Introduction
One of the best algorithms to start with when beginning to learn about machine learning is the K-nearest neighbors algorithm or K-NN. K-NN is considered by many people the simplest algorithms someone can learn. In this blog, I will be discussing the following questions:
- What is K-nearest neighbors?
- How does it work?
- How do I create a K-nearest neighbors model?
- What are the use cases for a K-nearest neighbors model?
By the end of the day, you should be able to answer to yourself all these questions and even hopefully code your very own K-NN model.
What is K-NN and when should I use it?
K-NN is a machine learning algorithm used most of the time for classifying new data. K-NN is good at classifying new data because it is a supervised machine learning algorithm which means it requires labeling for each row of data. When training data is passed into a K-NN model, the training data does not get modified, it’s simply stored into the model for it to be used for predictions. K-NN overall main goal is to retrieve new data and find the training data that is most similar to the new data and classify the new data. K-NN can be used in most classification cases/datasets. This blog contains the use of two classification datasets that were able to use K-NN fairly easily. You may not want to pick a fairly large dataset with K-NN because K-NN can become computationally intensive very quickly.

One of the best uses for the K-NN model is for a recommendation system. A recommendation system I wrote in the past uses a K-NN model by using Spotify data to recommend similar songs that a user have listened to in the past. This was possible because every song in Spotify has attributes and I used those attributes to create a K-NN model. When a user plugs in a song into the suggester, it finds the song’s attributes and plugs it into the K-NN model and it finds the top five Spotify songs that had similar attriubtes to the plugged in song. You can find that project here. Now we know what is K-NN is and when to use it, how does it work?
How does the algorithm work?
K-NN works by getting the euclidian distance from a test point to the k closest points to the test point. Euclidian distance is the distance from one point to another point in metric space. K-NN specifies how many neighbors to pick by using the letter k and k is defined by the user of the model.
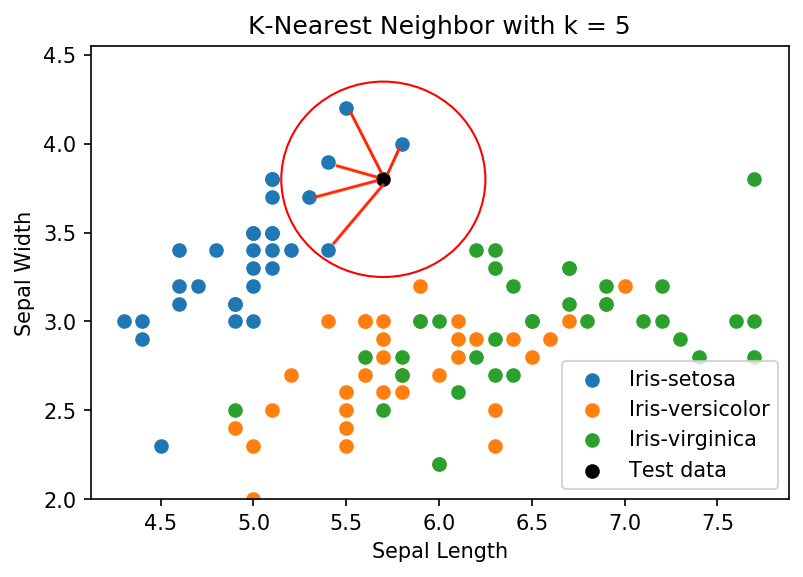
In the data visualization above, the black point is a data point from the test dataset. With k set to five, the model will find the five closest training points to the test set. These points are signaled by the red lines. Once the k closest points have been identified and selected, a voting process starts to determine what class to identify the test point. Since all the points that were selected were from the Iris-setosa class, the black test point predicted class is the Iris-setosa class. If for example, there was three Iris-setosa points and two Iris-virginica points, the predicted class would be Iris-setosa. Iris-setosa was the predicted class because there were more points selected for Iris-setosa than there were for Iris-virginica which is all determined by the algorithm’s voting process. To prevent having ties in the voting process (ex: k=2, 1 Iris-setosa, 1 Iris-virginica), it is best practice to pick an odd number for k so that there cannot be a tie in the classes selected. Now that we know what K-NN is and how the algorithm works, we can begin coding the model from scratch.
How do I create a K-NN model?
Before we start coding, lets plan out what we need to code:
- A class to hold our built K-NN model
- two variables two hold our X_train and y_train
- an attribute to set the value of k
- A class method to calculate the euclidian distance from two points
- we can use the numpy library to accomplish this
- A class method to fit our model on the class
- two parameters for X_train and y_train and set those passed in parameters as the attributes of the class
- A class method to predict the class(es) of the test data
- Get the distance of one test points to all test points
- pick the k closest points to the test point
- Get the classes of the k closest points
- Go through the voting process and determine what is the predicted class
- If there was multiple test rows plugged in, re-run the above steps
- return all the predicted classes
Now that we have our plan, lets start executing our plan into actual python code. Let’s begin by creating the K-NN class.
class K_NN:
X_train = None
y_train = None
def __init__(self, K):
self.K = K
We have created a class called K_NN with two variables called X_train and y_train and a constructor method with the parameter K. The two variables will hold our training data and the parameter K will hold the number of nearest neighbors we are going to collect. Now lets create the class method to calculate the euclidian distance from two points.
def euclidean_distance(self, row1, row2):
return np.linalg.norm(row1-row2)
In the method, row1 will take in an individual row of the training data and row2 will take in an individual test row from the test data. np.linalg.norm(row1-row2) is the calculation of the euclidian distance between two vectors. When we say .norm, we are telling np.linalg to return the distance of the two vectors. If you wanted to write that portion by hand, you could also write something like this np.sqrt(np.sum((v1 - v2) ** 2)) which does the same thing as the numpy method. Now let’s create the fit method of our class.
def fit(self,X_train,y_train):
self.X_train = X_train
self.y_train = y_train
This simply sets the passed in training data as the training data for the class object. This will be used in the predict method. Finally, lets write up the predict method. I’m going to break down the method into multiple steps since it’s our largest method.
def predict(self, pred):
predictions = []
for p in pred:
distances = []
for i, v in enumerate(self.X_train):
distance = self.euclidean_distance(v, p)
distances.append([distance, i])
We create an empty list called predictions that will hold all our predicted classes. for p in pred will iterate through all the plugged in test vectors and the distances list will hold all of our distances for that indiviudal test vector. for i, v in enumerate(self.X_train) will iterate through all the vectors in our training data and then we will get the distance of an individual training vector to our individual test vector. We will then append the distance to the distances list we created and also append the index of the training vector. This process happens to all of our training vectors and only one test vector. Next, lets sort the distances and pick out k distances.
sorted_distances = sorted(distances)
k_distances = sorted_distances[:self.K]
predict = [self.y_train[i[1]] for i in k_distances]
Now that we have all the distances from one test vector to all vectors in the training data, we can sort the distances from least to greatest sorted(distances). We then get the k closest points to the test vector sorted_distances[:self.k]. Since we saved the index of the training vector, we can then find what was the classification for each k points by doing [self.y_train[i[1]] for i in k_distances]. The last step for the predict method is to select the class for the test vector.
result = max(set(predict), key = predict.count)
predictions.append(result)
return predictions
max(set(predict), key= predict.count) will get the class that occured the most in the list and then that will get appended into the preditions list. If more than one test vector was passed in at once, it will go back up to the for p in pred for loop and do everything again until there is no more test vectors to iterate. Once everything is finished, it will return the predicted classes for every test vector the user plugged into the class object.
Now that we have all of our pieces of the class completed, we can now put all of this into one big class and create the complete K-NN class. I will add comments for each line to briefly describe what I explained above.
import numpy as np
class K_NN:
X_train = None
y_train = None
def __init__(self, K):
self.K = K
def fit(self,X_train,y_train):
self.X_train = X_train
self.y_train = y_train
def euclidean_distance(self, row1, row2):
return np.linalg.norm(row1-row2)
def predict(self, pred):
# empty list to hold each prediction
predictions = []
# iterates through each test row
for p in pred:
# empty list to hold distances for a specific test row
distances = []
# for loop to iterate through every row in the training set
for i, v in enumerate(self.X_train):
# calculate the euclidean distance between a training row
# and test row
distance = self.euclidean_distance(v, p)
# append the distance to the distances list
distances.append([distance, i])
# sort the distances from least to greatest
sorted_distances = sorted(distances)
# take only smallest k distances
k_distances = sorted_distances[:self.K]
# Get the predicted classification
predict = [self.y_train[i[1]] for i in k_distances]
# Get the most frequent predicted element from predict
result = max(set(predict), key = predict.count)
# Append the result to the predictions list
predictions.append(result)
return predictions
Congratulations! You have coded your very own K-NN model! Now that this is complete, we can test it out with actual data.
Testing the K-NN Class
To test the class we created, we will use a dataset from UCI that contains data that tells us if a patient has heart disease or does not. This is what the data looks like. 0 means that the patient has heart disease and 1 does not.
First, we will import the dataset csv into our python module and identify our features (x) and our target (y).
df = pd.read_csv("heart.csv")
x = np.array(df.drop(columns=['target']))
y = np.array(df['target'])
Next, we will split our data into training and testing datasets. We will train our model off the training dataset and test our model off the testing dataset. We will then standardize our X_train and X_test to get all of our features on the same scale.
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.33, random_state=42)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
Now that our data pre-processing is done, we can now utilize the class we made. First thing is to instantiate the object with the class we created with the K value we want. For this example, I used the k value seven.
model = K_NN(K=7)
Once our model has been created, we can then fit our training data to the class object and run a prediction off the test data we created above.
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
We can print out y_pred to see all of our predicted classes.
print(y_pred)
output: [0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0]
For each row/vector of the test data, we got a predicted class. With the predictions, we can now test how accurate our model was by comparing the y_pred variable to the actual labels from y_test.
acc = accuracy_score(y_test, y_pred)
print(f"By hand accuracy: {acc}")
# Output: By hand accuracy: 0.86
When comparing our predictions to the actual classes of the test data, our model predicted 86% of the classes correctly. Now that we know that our model is working, how does it compare to a sklearn K-NN model? We can test this by running the same datasets we created above through a sklearn model.
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=7)
neigh.fit(X_train, y_train)
sklearn_pred = neigh.predict(X_test)
print(f"Sklearn model accuracy: {accuracy_score(y_test, sklearn_pred)}")
# Output: Sklearn model accuracy: 0.86
Since the accuracy scores of both by hand and sklearn models are the same, we can say that our model we created works very similarly or if not the same as the sklearn model.
Conclusion
By reading this post, you have learned what is K-NN, how the algorithm works, how to execute a K-NN algorithm from scratch, and the use cases of a K-NN model. K-NN is one of the most fundamental machine learning algorithms a data scientist can learn. It can classify just about any sort of labeled data in a very quick manner. Thanks for reading and I hope this post was helpful to you in some way!